Systems of equations

Systems of equations

In this article, I will explain to you how to solve systems of equations in a generic way.
The starting point, there are as many equations as unknowns.
Finally, I will show you how some things can be implanted in Excel.

The school method

If you took math in high school you have probably done this before.
But I get that that could have faded.
School taught you that there are two methods for solving systems of equations:

1. Substitution
2. Elimination

Let’s take a look at both methods using this easy example:

Take a look at this system:

I: 2x-2y=-2
II: 3x+2y-7=0

To simplify things, let’s make the bottom one (II) in the same order as the first one (I):

I: 2x-2y=-2
II: 3x+2y=7

First, the substitution method: Let’s solve for x, or for y.

I can rewrite equation I to 2x=2y-2 and if I divide all the factors by 2: x=y-1

Now I can fill in the found x in equation II:

3(y-1)+2y=7 ==> 3y-3+2y=7 ==> 5y=10 ==> y=2

We know (3 lines back) that x=y-1, so x=2-1=1.

And with this, we have solved the system.

The second method is elimination:

I: 2x-2y=-2
  II: 3x+2y= 7  (I’m going to add I and II)
I+II: ————————+
      5x+0 = 5

Y has immediately disappeared: So 5x=5 ==> x=1; fill in in I (or II): 2(1)-2y=-2 ==> -2y=-4 ==> y=2.
System solved again.

In general, the second method is (a little) faster, even though you often need to ‘rebuild’ one or both of the equations to make them easier to add or subtract.

The methods will get harder when there are more equations and more unknowns.
We are going to have to simplify things a little. To do this, we will start working with matrices. We will throw all the unnecessary ballast overboard.

Matrix row reduction

In the example, only the coefficients and loose numbers are interesting because we calculate with those. The xs and ys are only making things difficult in that progress (not even speaking of a system with 30 equations with 30 unknowns, because we don’t have enough letters to use and have to start indexing etc.)

We write the system down like a matrix:

2 -2 | -2
3  2 |  7

in which the coefficients stand in front of the vertical line and the loose numbers behind it.
The first column contains the xs and the second the ys.
The trick is to turn this matrix into a so-called identity matrix (or unit matrix); a matrix where the main diagonal only contains the number 1, and all the other numbers are 0. This means all the numbers behind the vertical line are the solutions.

Here’s a generic algorithm known as the Gaussian elimination:

In the first round, the first element on the first row is set to 1, by multiply all the numbers on the first row with the inverse of the first element of the first row (the reciprocal) followed by:
All the other rows are subtracted by the first one with a factor corresponding to the value of the first element of the other rows.

This is repeated for all the rows where the first one is replaced by the second one, the third one, etc.
This means that for n equations with n unknowns, you need n rounds.

Back to our example:
So we have:

2 -2 | -2
3  2 |  7

Round 1:

Multiply I with 0,5 (=1/2):

1 -1 | -1 ; now subtract 3*I from II, so II-3*I:
0  5 | 10

Round 2:

Multiply II with 0,2 (=1/5):

…
0 1 | 2 ; now subtract -1*II from I , so I-1*II, or I + II

1 0 | 1
0 1 | 2

Now you’ll find the solutions of x (first column) and y (second column) behind the vertical line.

Moreover, the matrices need to be neatly placed between parentheses, but this is very awkward, typographically speaking.

Excel knows a couple of matrix-functions but not one to apply the Gaussian elimination.

Luckily, the new version (2017) of hj GSO ft’s Excel-Adequate offers a solution.

Solve System Of Equations wizard

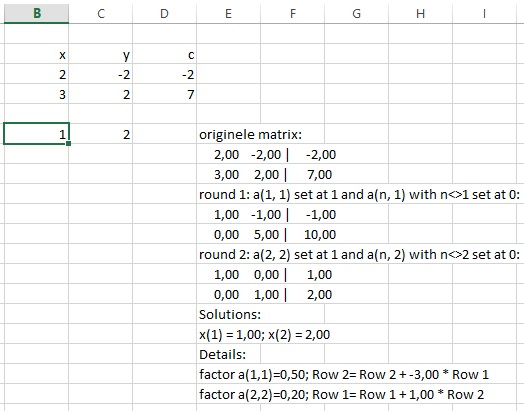
First, put up a worksheet with the coefficients:

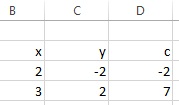
Click in the tab HJGSoft in the ribbon on the button Pick a wizard and click on the option Solve System Of Equations.

You will see the following window:

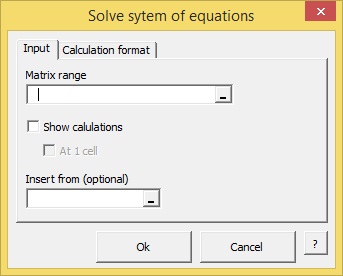
The window contains two tabs. Fill the first one in as follows:

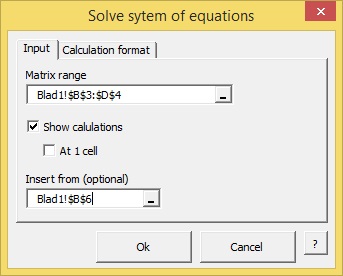
Now click on the tab Layout Calculation and make the desired choices:

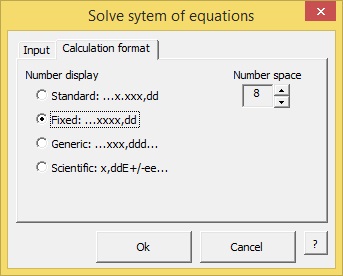
Press OK and see the result:

 

SolveSystemOfEquations is part of the Excel-Adequate of HJGSoft. For more information go to the page Excel Adequate. You can here download the tool and can try it out for free for 10 days.